할리데이 일반물리학(대학물리학) #벡터 #스칼라

벡터는 수학적인 개념인데, 물리에서 벡터를 빼놓고 생각을 할 수 없을 만큼 벡터는 중요합니다.
벡터를 시작하기 전에 벡터 하면 떠오르는 대상이 스칼라가 있습니다. 벡터와 스칼라를 많이 비교하게 되는데, 수학적으로 벡터와 스칼라를 구분하는 방법부터 배워 보도록 하겠습니다.

1. 벡터와 스칼라

 ① 스칼라(scalar)

     ㉠ 크기만. 하나의 숫자로 표시

     ㉡ 음의 스칼라: 크기가 0보다 작다.

     ㉢ 스칼라량의 예: 온도(T), 압력(p), 에너지(E),  질량(m), 시간(t)

 ② 벡터(vector)

     ㉠ 크기와 방향

     ㉡ 벡터의 크기: 0보다 같거나 크다.

     ㉢ 음의 벡터: 반대 방향

     ㉣ 벡터량의 예: 변위, 속도, 가속도

 ③ 변위 벡터의 예 

세 가지 경우 모두 크기와 방향이 같은 하나의 변위 벡터이다.

두 점을 잇는 세 가지 경로의 이동거리는 다르지만 변위는 모두 같다.

2. 벡터의 덧셈과 뺄셈: 기하학적 방법

(1) 벡터의 덧셈

 

 ① 평행사변형법                                   ② 삼각형법

 

 ③ 교환법칙:

 

 ④ 결합법칙: 

 

 

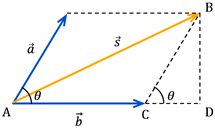
 ⑤ 합벡터의 크기

 

⇒

 

 

삼각형 ABC에서 코사인 법칙을 이용한다.

 

또는 삼각형 ABD에서 피타고라스 정리를 이용한다.

 

 

(2) 벡터의 뺄셈

① -b:b와 크기는 같고 방향이 반대. 

 

 

② 벡터의 뺄셈:

 

 

 

 

 

3. 벡터의 성분

 

 ① 벡터의 분해

 

 

 

 

 

 

② 벡터의 성분:

 

 

⇔

 

 

 

 

 

 

 

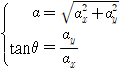
0 : 양의 x축으로부터 반시계 방향의 각